FFT補零可以提高頻率分辨率嗎?
- 瀏覽次數:23758次
- 發布時間:2014/3/19 11:27:32
- 作者:銀河電氣
經常看到
FFT補零是否可以提高
頻率分辨率的討論,事實上,只要我們明確
傅里葉變換的本質,就很容易判斷補零對傅里葉變換的影響。
從根本上講,傅里葉變換僅僅是一種變換而已。所謂變換,是指經過傅里葉變換,得到的是輸入信號的另外一種表現形式。
具體上講,傅里葉變換是一種時域與頻域之間的轉換,傅里葉變換的輸入是時域信息,輸出是頻域信息。利用傅里葉變換,可以通過時域信息得到頻域信息,反之,得到的頻域信息通過傅里葉逆變換,可以得到與傅里葉變換輸入相同的時域信息。
一句話總結,傅里葉變換的輸入與輸出,具有不同的表現形式,但是,都表示同一個信號。
FFT補零主要發生在兩種場合:
1、傅里葉點數不是2的N次冪,通過補零得到2的N次冪個點,這種情況下,一般補零的數量不會太多。
2、由于傅里葉變換得到的頻域信息的頻率分辨率與傅里葉變換輸入的時域信息代表的時間長度的倒數相等。因此,有人希望通過給時域信息補零,延長時域信息代表的時間,從而提到頻域信息的分辨率。這種情況下,補零的數量取決于希望達到的頻率分辨率。
就數學上講,上述兩種情況下,FFT輸出的頻率分辨率都提高了。
例如:采樣頻率為1024Hz,采樣得到的序列包含1000點,1000個點數據不能進行FFT變換,若采用DFT變換,DFT輸出的頻率分辨率為1.024Hz。補上24個零,得到1024點的序列,進行FFT變換,FFT輸出的頻率分辨率為1Hz,頻率分辨率由1.024Hz提高到了1Hz;若補上1048個零,序列代表的時間長度為2S,FFT輸出的頻率分辨率0.5Hz,頻率分辨率由1Hz進一步提高到0.5Hz。
這樣看來,FFT補零的確可以提高頻率分辨率,并且,只要你愿意,可以無限的提高!
值得注意的是,零也是數據,在FFT變換時,算法并不能識別哪些為有用,哪些為無用,補零就是改變了FFT的輸入,輸出自然也會改變。
FFT補零得到的頻譜,代表的是補零后的波形,而補零后的波形與原始波形是不一樣的,不是我們真正關心的波形。換言之,FFT補零的確可以提高頻率分辨率,但是,FFT輸出結果誤差增大了,當補零數過多時,誤差達到不可接受的程度時,就是錯誤了。
傅里葉變換得到的頻譜中,最低頻率分量的頻率f0等于傅里葉時間窗的長度(輸入序列代表的時間長度)的倒數。頻率為f0的頻率分量稱為基波,若被測波形不是頻率為f0的正弦波,那么,傅里葉頻譜中,必然還包括與該頻率成整倍數的其它頻率分量,這些分量稱為諧波。
看下面這個具體的例子:
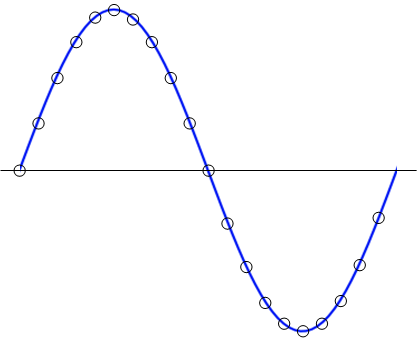
被測波形為50Hz正弦波,采樣率為1000Hz,采樣時間為20mS,得到圖1所示的20個采樣點的序列,采用DFT對該序列進行變換,頻譜中,只有50Hz的譜線,頻率分辨率為50Hz。
這是正確的結果,可以反映輸入波形的特征。
WP4000變頻功率分析儀的基波測量和諧波分析就是采樣的方式,一方面確保對被測信號進行
整周期截斷,另一方面由于采用DFT,序列點數不受2的N次冪的限制。
圖1. 50Hz正弦波的20個原始采樣點
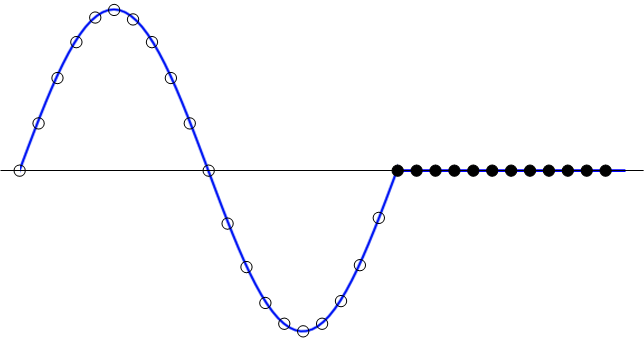
圖2. 補零后的32個采樣點
如果我們采用FFT,由于20不等于 2的N次冪,我們補上12個零,得到如圖2的32點的序列。
對比圖2和圖1,我們發現,補零后FFT的分析對象變了。這是一個什么樣的對象呢?
由于實際信號一般是無限長序列,而FFT針對的序列總是有限長的,因此,傅里葉變換基于這樣一種假設,假設實際信號以輸入的有限長序列為周期,并按照該周期進行周期延拓。我們將圖1和圖2的序列進行周期延拓后,得到圖3和圖4的序列。
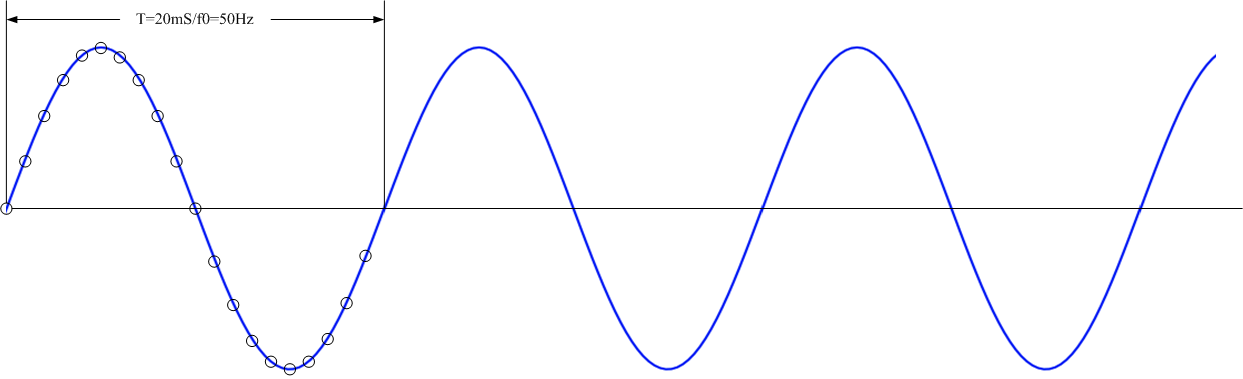
圖3. 原樣本序列周期延拓后的無限長序列
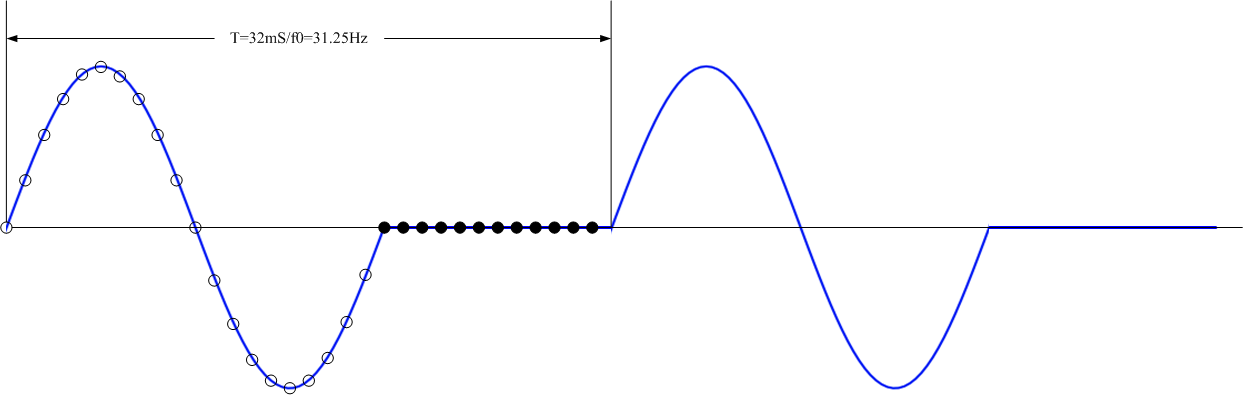
圖4. 補零后序列周期延拓后的無限長序列
圖中可以直觀地看出,圖3是周期為20mS,頻率為50Hz的正弦波,而圖4是周期為32mS,頻率為31.25Hz的特殊波形。就時域圖中,我們看不出其頻譜,但是,依據傅里葉論斷,該波形對應的頻譜僅包含頻率為31.25Hz的基波及頻率為31.25Hz整數倍的諧波,一定不包含50Hz的頻率分量。
圖3的頻率的頻率分辨率為50Hz,圖4的頻率的頻率分辨率為31.25Hz。頻率分辨率確實提高了,但是,補零后得到的頻譜(圖4對應的頻譜)不是我們想要的!
一句話:FFT補零可以提高頻率分辨率,但是,補零得到的不是我們需要的頻譜。
【擴展閱讀】:
作者:AnyWay中國