測量不確定度的A類評定
- 瀏覽次數:10920次
- 發布時間:2017/2/24 21:42:41
- 作者:ly_yinhe
測量不確定度的A類評定簡稱A類評定,是指對在規定測量條件下測得的量值用統計分析的方法進行的測量不確定度分量的評定。下面本文主要根據測量不確定度的評定與表示介紹測量不確定度的A類評定相關方法及計算。
對被測量進行獨立重復觀測,通過所得到的一系列測得值,用統計分析方法獲得試驗標準偏差s(x),當用算術平均值x作為被測量估計值時,被測量估計值的A類標準不確定度按式1計算:
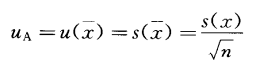
……1
標準不確定度的A類評定的一般流程見下圖1。
圖示:標準不確定度的A類評定流程圖
一貝塞爾公式法
在重復性條件或復現性條件下對同一被測量獨立重復觀測n次,得到n個測得值
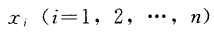
被測量X的最佳估計值時n個獨立測得值的算術平均值x,按公式2計算:
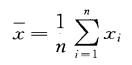
……2
單個測得值xk的實驗方差s^2(xk)按式3計算:
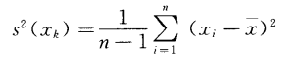
……3
單個測得值xk的實驗標準偏差s(xk),按公式4計算:
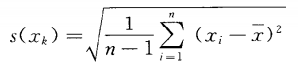
……4
公式4就是貝塞爾公式,自由度ν為n-1。實驗標準偏差s(xk)表征了測得值x的分散性,測量重復性用s(xk)表征。
被測量估計值x的A類標準不確定度uA(x)按公式5計算:
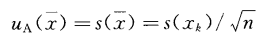
……5
A類標準不確定度uA(x)的自由度為實驗標準偏差s(xk)的自由度,即ν=n-1。實驗標準偏差s(x)表征了被測量估計值x的分散性。
二極差法
一般在測量次數較少時,可采用極差法評定獲得s(xk)。
在重復性條件或復現性條件下,對Xi進行n次獨立重復觀測,測得值中的最大值與最小值之差稱為極差,用符號R表示。在Xi可以估計接近正態分布的前提下,單個測得值xk的試驗標準差s(xk)可按公式6近似地評定:
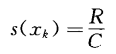
……6
式中:
R——極差;
C——極差系數。
極差系數C及自由度ν可查得表1得到。
表1:極差系數C及自由度ν
被測量估計值的標準不確定度按式7計算:
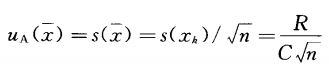
……7
三測量過程合并標準偏差的評定
對一個測量過程,采用核查標準和控制圖的方法使測量過程處于統計控制狀態,若每次核查時的測量次數為nj(自由度為νj),每次核查時的實驗標準偏差為sj,共核查m次,則統計控制下的測量過程的A類標準不確定度可以用合并實驗標準偏差sp表征。測量過程的實驗標準偏差按公式8計算:
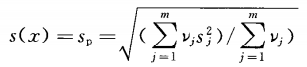
……8
若每次核查的自由度相等(即每次核查時測量次數相同),則合并樣本標準偏差按公式9計算:
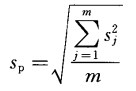
……9
式中:
Sp——合并樣本標準偏差,是測量過程長期組內標準偏差的統計平均值;
Sj——第j次核查時的實驗標準偏差;
m——核查次數。
在過程參數sp已知的情況下,由該測量過程對被測量X在同一條件下進行n次獨立重復觀測,以算術平均值x為測量結果,測量結果的A類標準不確定度按公式10計算:
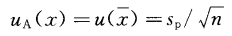
……10
四合并樣本標準偏差的評定
例如使用同一個計量標準或測量儀器在相同條件下檢定或測量示值基本相同的一組同類被測件的被測量時,可以用該一組被測件的測得值作測量不確定度的A類評定。
若對每個被測件的被測量Xj在相同條件下進行n次獨立測量,測得值為xi1,xi2,……xin,其平均值為xi;若有m個被測件,則有m組這樣的測得值,可按公式11計算單個測得值的合并樣本標準偏差:
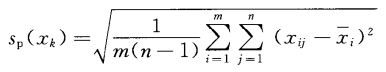
……11
式中:
I——組數,i=1,2,……,m。
J——每組測量的次數,j=1,2,……,n。
公式10給出的sp(xk),其自由度為m(n-1)。
若對每個被測件已分別按n次重復測量算出了其實驗標準偏差si,則m組測得值的合并樣本標準偏差sp(xk)可按公式12計算:
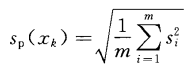
……12
當實驗標準偏差si的自由度均為ν0時,公式12給出的sp(xk)的自由度為mν0。
若對m個被測量Xi分別重復測量的次數不完全相同,設各為ni,而Xi的實驗標準偏差s(xi)的自由度為νi,通過m個si與νi可得sp(xk),按公式13計算:
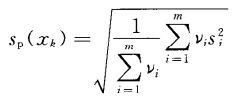
……13
由公式13給出的sp(xk)的自由度為
由上述方法對某個被測件進行n’次測量時,所得測量結果最佳估計值的A類標準不確定度為:
五預評估重復性的評定
在日常開展同一類被測件的常規檢定、校準或檢測工作中,如果測量系統穩定,測量重復性無明顯變化,則可用該測量系統以與測量被測件相同的測量程序、操作者、操作條件和地點,預先對典型的被測件的典型被測量值進行n次測量(一般n不小于10),由貝塞爾公式計算出單個測得值的實驗標準偏差s(xk),即測量重復性。在對某個被測件實際測量時可以自測量n’(1≤n’<n),并以n’次獨立測量的算術平均值為被測量的估算值,則該被測量估計值由于重復性導致的A類標準不確定度按公式14計算:
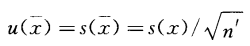
……14
用這種方法評定的標準不確定度的自由度仍為ν=n-1.應注意,當懷疑測量重復性有變化時,應及時重新測量和計算實驗標準偏差s(xk)。

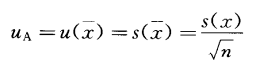 ……1
……1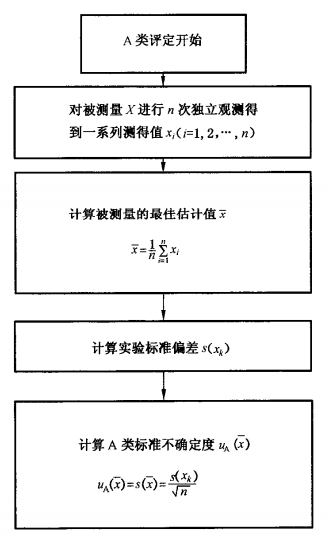
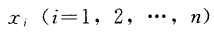 被測量X的最佳估計值時n個獨立測得值的算術平均值x,按公式2計算:
被測量X的最佳估計值時n個獨立測得值的算術平均值x,按公式2計算: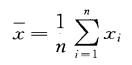 ……2
……2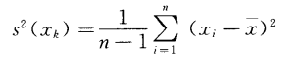 ……3
……3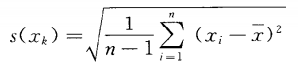 ……4
……4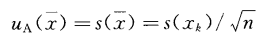 ……5
……5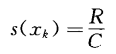 ……6
……6
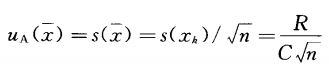 ……7
……7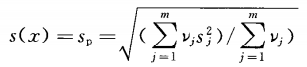 ……8
……8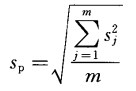 ……9
……9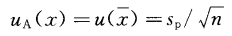 ……10
……10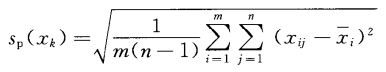 ……11
……11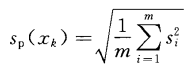 ……12
……12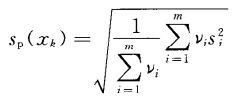 ……13
……13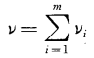
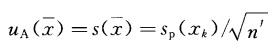
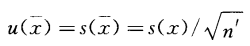 ……14
……14